发布日期: 2020-05-07

1361.验证二叉树

二叉树上有 n 个节点，按从 0 到 n - 1 编号，其中节点 i 的两个子节点分别是 leftChild[i] 和 rightChild[i]。

只有所有节点能够形成且只形成一颗有效的二叉树时，返回 true；否则返回 false。

如果节点 i 没有左子节点，那么 leftChild[i] 就等于 -1。右子节点也符合该规则。

注意：节点没有值，本问题中仅仅使用节点编号。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/validate-binary-tree-nodes
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

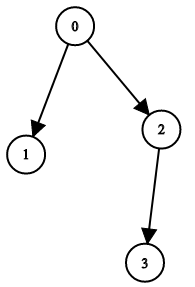
输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
输出：true

输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
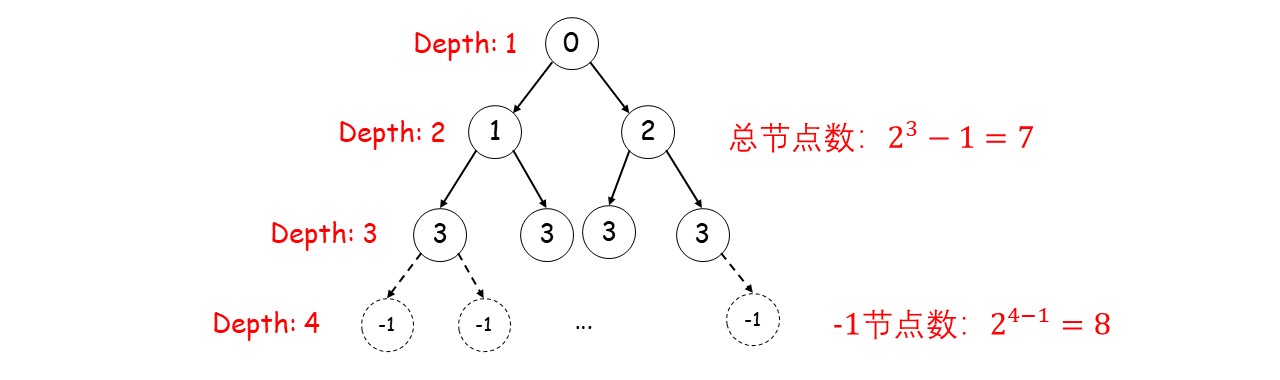
输出：false

以满二叉树为例，我们知道一个深度为 nn 的二叉树有如下特点：

一共有2^n-1个节点
深度为n的叶子节点为2^(n-1)个节点
叶子节点下面的节点为题目中的-1的节点，深度为n+1，个数为2^(n+1-1)=2^n个节点
所以-1 的节点个数比总结点个数多1

class Solution(object):
   def validateBinaryTreeNodes(self, n, leftChild, rightChild):
       return (leftChild + rightChild).count(-1) == n + 1

方法一：连通性判定

官方题解:

我们将验证二叉树的过程分为两步：第一步找到二叉树的根节点，第二步从根节点开始对二叉树进行遍历，判断其是否为一颗有效的二叉树。

在第一步中，为了找到根节点，我们需要用数组 indeg 存放所有节点的入度，这是因为只有入度为 0 的点才能是根节点。我们遍历数组 leftChild 和 rightChild，如果数组中的某个元素 x 不为 -1，那么就表示有一条边指向节点 x，节点 x 的入度 indeg[x] 增加 1。在遍历完数组 leftChild 和 rightChild 后，我们在数组 indeg 中找到一个满足 index[root] == 0 的节点 root，即为二叉树的根节点。

如果有多个满足 index[root] == 0 的节点呢？在这种情况下，这 n 个节点一定不是一颗有效的二叉树。我们把这个问题放在第二步来考虑，而在第一步中，我们先不处理这个问题。

在第二步中，我们从根节点开始进行深度优先搜索或广度优先搜索，判定这 n 个节点的连通性，这是因为当这个 n 个节点是一颗有效的二叉树时，所有的节点会恰好被遍历一次。如果某一个节点被遍历了超过一次（有不止一个父节点）或零次（不连通），那么这 n 个节点都不是一颗有效的二叉树。我们可以使用哈希集合（HashSet）seen 来存放所有被遍历过的节点，如果在搜索时遍历到了 seen 中出现的节点，那么说明该节点被遍历了超过一次。如果在搜索完成后，seen 中的节点个数少于 n，那么说明有些节点没有被遍历过。

回到第一步中遗留的那个问题，如果有多个满足 index[root] == 0 的节点 r1, r2, …，那么我们可以任意选择一个节点，例如 r1，作为根节点。在搜索时，由于节点 r2, … 的入度为 0，因此不可能被遍历到。这样在搜索结束后，seen 中的节点个数一定少于 n。

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/validate-binary-tree-nodes/solution/yan-zheng-er-cha-shu-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。


class Solution {
public:
   bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {
       vector<int> indeg(n);
       for (int i = 0; i < n; ++i) {
           if (leftChild[i] != -1) {
               ++indeg[leftChild[i]];
           }
           if (rightChild[i] != -1) {
               ++indeg[rightChild[i]];
           }
       }

       int root = -1;
       for (int i = 0; i < n; ++i) {
           if (!indeg[i]) {
               root = i;
               break;
           }
       }
       if (root == -1) {
           return false;
       }

       unordered_set<int> seen;
       queue<int> q;
       seen.insert(root);
       q.push(root);

       while (!q.empty()) {
           int u = q.front();
           q.pop();
           if (leftChild[u] != -1) {
               if (seen.count(leftChild[u])) {
                   return false;
               }
               seen.insert(leftChild[u]);
               q.push(leftChild[u]);
           }
           if (rightChild[u] != -1) {
               if (seen.count(rightChild[u])) {
                   return false;
               }
               seen.insert(rightChild[u]);
               q.push(rightChild[u]);
           }
       }

       return seen.size() == n;
   }
};